Kvantitativní SPM měření

Morfologie povrchu a měření mechanických vlastností

Pokud se zaměříme na objekty větší než cca 10 nanometrů, je kvantitativní měření tvaru povrchu patrně nejsnazší disciplínou rastrovací mikroskopie. Měřená data jsou sice ovlivněna konvolucí hrotu s povrchem a mohou být zatížena různými systematickými chybami (kalibrace) nebo náhodnými jevy (šum), metody dektece a případné kompenzace těchto jevů jsou však všeobecně známé a mohou být provedeny v podstatě v každém SW pro analýzu SPM dat (např. Gwyddion).

Pokud chceme měřit objekty, které jsou menší, situace se komplikuje - již nemůžeme předpokládat, že objekty jsou nekonečně tuhé a měření musíme doplnit numerickým modelováním interakce hrotu s povrchem, zahrnujícím jak síly působící mezi hrotem a povrchem, tak vratné i nevratné deformace obou těles. Pouze tento přístup nám může zprostředkovat informace o příspěvcích do rozpočtu nejistot, které jsou dány kvantově mechanickými jevy mezi hrotem a povrchem.

Nejpřirozenější cestou, jak numericky obsáhnout jevy mezi hrotem a povrchem, je využít některé z ab-initio metod, například metody funkcionálu hustoty (DFT). Pro systém s omezeným počtem částic tak můžeme spočítat jak síly, tak vzájemné polohy a výsledné tvary jednotlivých těles. Na našem pracovišti pro tyto účely spolupracujeme s Fyzikálním ústavem AVČR a využíváme program Fireball, který je pro výpočty v oboru rastrovací mikroskopie do velké míry uzpůsoben. Výsledkem výpočtů jsou informace vedoucí k stanovení nejistot při zobrazování různých nanometrických objektů a sil mezi nimi působících [1,2].

V mnoha případech potřebujeme analyzovat podstatně větší struktury, než by bylo reálné počítat pomocí DFT. Musíme tedy snížit nároky na správnost výpočtů a použít přibližnou metodu, například klasickou molekulární dynamiku. Kvantově mechanické působení mezi částicemi tím redukujeme na jednoduché analytické potenciály, což nám umožňuje provádět výpočty ne na tisících atomech, ale na stovkách milionů. Kromě nanometrických struktur tak můžeme simulovat i prostorově rozsáhlejší jevy, například v oboru nanoindentace [3]. Na oddělení nanometrologie využíváme vlastní software pro molekulární dynamiku, který je možné provozovat nejen na procesoru osobního počítače, ale i na grafické kartě, což výrazně zvyšuje rychlost výpočtu.

Konfigurace při DFT/MD výpočtech interakce mezi AFM hrotem a fulerenem C60	Simulace vpichu do krystalu zlata o různých povrchových orientacích

Termální, elektrické a magnetické jevy

Při kvantitativní analýze dat získaných různými speciálními SPM metodami, jako jsou elektrická či termální mikroskopie, je nutné provádět numerickou analýzu téměř vždy. Často je nutné vyvíjet i speciální metody pro samotný sběr dat, které by bylo možné s numerickými experimenty srovnat. Typicky používanými numerickými metodami jsou metoda konečných prvků a metoda konečných diferencí, kterými řešíme rovnice vhodné pro popis konrétního měření (Poissonova rovnice pro tepelné a elektrostatické jevy, Landau-Lifschitz-Gilbertova rovnice pro magnetické jevy).

Pro výpočty těchto jevů používáme jak vlastní software, tak různé volně šiřitelné produkty, jako jsou programy Sfepy, Elmer, či OOMMF.

V některých případech je množství informací o vlastnostech sestavy hrot-povrch tak malé, že je problém numerický model vůbec sestavit. V takovém případě je možné použít některou přibližnou metodu, například predikci signálu pomocí neuronové sítě [4]. Takový přístup je obzvlášť vhodný pro studium různých artefaktů, kterých jsou SPM měření plná.

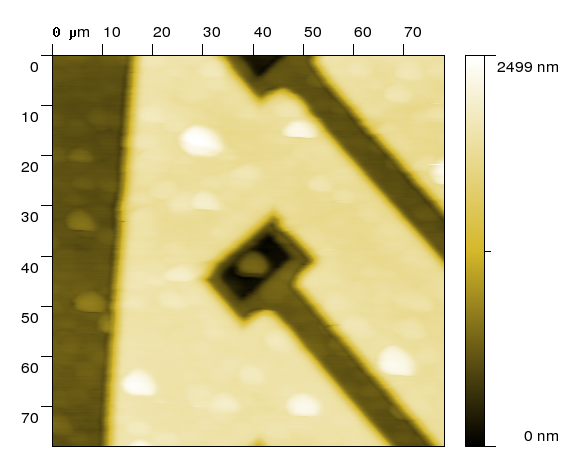
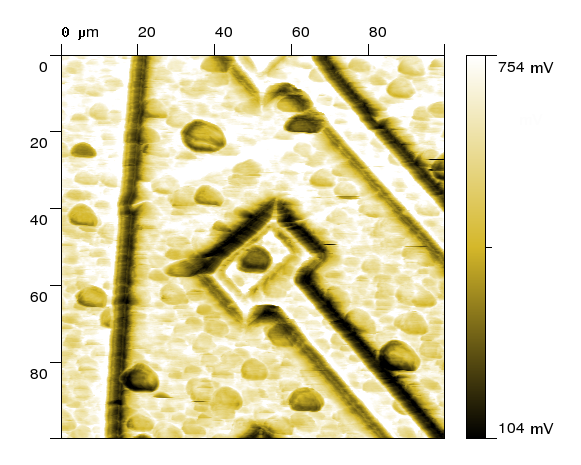
Morfologie povrchu	Měřený termální signál (SThM)	Predikovaný termální signál (neuronová síť)

Optická mikroskopie

V případě rastrovací optické mikroskopie v blízkém poli je v podstatě nemožné provést kvantitativní měření bez numerické analýzy (a v mnoha případech je to nemožné i s ní). Pro tyto účely využíváme metodu FDTD (Finite Difference in Time Domain), pomocí které můžeme simulovat rozložení elektromagnetického pole v prostoru mezi hrotem a povrchem a následně i ve vzdáleném poli, kde je typicky umístěn detektor [5]. Tato metoda je vhodná nejen pro analýzu nejistot při měření pomocí techniky SNOM, ale i pro pochopení dat naměřených na různých neznámých strukturách [6].

Pro účely FDTD výpočtů používáme vlastní software, také uzpůsobený pro provoz na grafické kartě. Tento software postupně modifikujeme do podoby volně šiřitelného balíku pro optické výpočty Gsvit. Využití metody FDTD je mnohem širší než k pouhému zpracování SNOM snímků, jen na našem pracovišti ji využíváme také pro analýzu dat z měření rozptylu [7], analýzu solárních článků [8] nebo mikrostruktur vytvořených litografií [9].

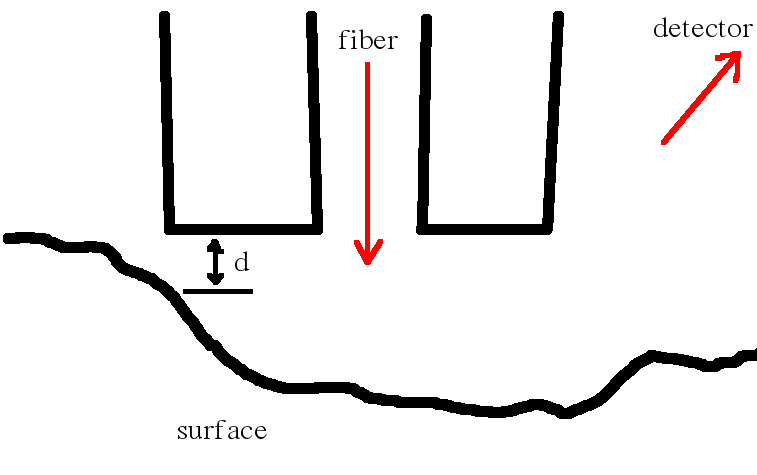
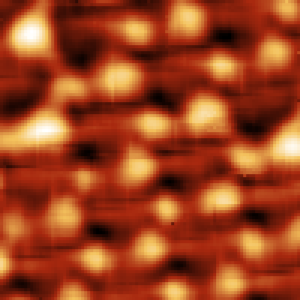
Geometrie FDTD výpočtu	Měřená morfologie (hliníkové ostrůvky)	Simulovaný reflexní SNOM snímek

[1]A. Campbellová, P. Klapetek a M. Valtr, Tip-sample relaxation as a source of uncertainty in nanoscale scanning probe microscopy measurements, Measurement Science and Technology, 20, 2009, 084014
[2]A. Campbellová, M. Ondráček, P. Pou, R. Pérez, P. Klapetek and P. Jelínek, 'Sub-atomic' resolution of non-contact atomic force microscope images induced by a heterogeneous tip structure: a density functional theory study, Nanotechnology 22, 2011, 295710
[3]A. Campbellová, P. Klapetek, V. Buršíková, M. Valtr, J. Buršík, Small-load nanoindentation experiments on metals, Surface and Interface Analysis, 42 2010, 6, pp 766-769
[4]P. Klapetek, I. Ohlídal and J. Buršík: Application of scanning thermal microscopy in analysis of the geometry of patterned structures, Surface and Interface Analysis 38 (2006) 383-387
[5]P. Klapetek, M. Valtr: Near field optical microscopy simulations using graphics processing units, Surface and Interface Analysis 2010, 42, pp 1109-1113
[6]P. Klapetek, J. Bujdák, J. Buršík: Near-field scanning optical microscopy local luminescence studies of rhodamine dye, Central European Journal of Physics 8 (2010) 312-317.
[7]P. Klapetek, M. Valtr, A. Poruba, D. Nečas, M. Ohlídal, Rough surface scattering simulations using graphics cards, Applied Surface Science 2010, 256, pp 5640-5643
[8]A. Poruba, P. Klapetek, J. Holovský, A. Purkrt and M. Vaněček, Experimental Limits of Light Capture in Thin Film Silicon Devices, MRS Proceedings, Vol. 1101, 2008, DOI: http://dx.doi.org/10.1557/PROC-1101-KK02-03
[9]P. Klapetek, T. Wágner and J. Orava, Electromagnetic field distribution modelling in microlenses fabrication process, Journal of Physics and Chemistry of Solids, Volume 68, Issues 5-6, May-June 2007, Pages 887-890

(c) CMI 2012